Event sort

This page discusses the details of the using and implementing the event sorting approach.

from typing import Callable
from datetime import datetime
from matplotlib import pyplot as plt

Example

Consider series of periods visualised on the following picture.

Suppose you need to identify the time interval with the most simultaneous processes. The event-sort approach is a special solution this type of tasks.

---

The following cell shows the program’s implementation and prints its output.

START, END = 0, 1
intervals = [(30, 300), (100, 240), (180, 360), (360, 550)]

events: list[tuple[int, int]] = []
for start, end in intervals:
    events.append((start, START))
    events.append((end, END))

events.sort()

max_count = 0
best_interval = (0, 0)
active_intervals = 0
for i, (e_moment, e_type) in enumerate(events):
    if (active_intervals > max_count) and (i != 0):
        max_count = active_intervals
        best_interval = (events[i - 1][0], e_moment)

    if e_type == START:
        active_intervals += 1
    else:  # e_type == END
        active_intervals -= 1


print(best_interval)

(180, 240)

Two passes

There are some tasks for which the event-sorting approach can lead to quadratic complexity. These are tasks that require returning a set of objects corresponding to a specific state - so at each step, the conditions are checked and the current set is copied to the result set. In the worst case, the result set may need to be updated at every event, which results in quadratic complexity with respect to the number of events.

There are several approaches that can be used in specific cases, but the most universal solution is to go through the events twice: first, to determine the positions where the conditions are met, and second, to find the appropriate result based on those positions.

---

Consider the following task: given a set of time periods \((t_i, t'_i)\), find the set of indices of the periods that fall within the time interval where the maximum number of periods overlap.

The following cell defines the function that generates the events, as this code is shared by both solutions.

START, END = 0, 1

def construct_events(intervals: list[tuple[int, int]]) -> list[tuple[int, int, int]]:
    events: list[tuple[int, int, int]] = []
    for i, (start, end) in enumerate(intervals):
        events.append((start, START, i))
        events.append((end, END, i))
    return events

The following cell defines the basic solution. As previously described, it simply copies the best set of the items wheather a better solution is found.

def basic_solution(intervals: list[tuple[int, int]]) -> set[int]:
    events = construct_events(intervals)
    events.sort()

    intervals_set: set[int] = set()
    ans: set[int] = set()

    for _, e_type, i in events:
        if e_type == START:
            intervals_set.add(i)
        else:  # e_type == END
            intervals_set.remove(i)
        if len(intervals_set) > len(ans):
            ans = intervals_set.copy() # Notice that we copy the set here
    return ans

The next code uses the basic_solution function.

basic_solution([(30, 50), (100, 240), (180, 360), (360, 550)])

{1, 2}

But consider a really specific kind of input, as visualized in the following picture:

With each event, a new element is added to the set. Therefore the algorithm is required to copy the accumulated elements to the answer for each of first five iterations.

The following cell defines a function that generates this type of input at a defined scale.

def generate_case(n: int) -> list[tuple[int, int]]:
    return [(i, n + i)for i in range(n)]

The next code implements the performance estimation function, that gradually increases the arrays generated by generate_case, and measures the time it takes to process the data.

def estimate_time_complexity(target: Callable[[list[tuple[int, int]]], set[int]]) -> list[tuple[int, float]]: 
    timings: list[tuple[int, float]] = []
    for i in range(1, 2_000):
        res: list[float] = []
        for _ in range(5):
            start = datetime.now()
            target(generate_case(i))
            end = datetime.now()
            res.append((end - start).total_seconds())
        timings.append((i, sum(res)/len(res)))
    return timings

The execution time progress related to the number of process intervals is displayed in the following cell.

timings_basic = estimate_time_complexity(basic_solution)
plt.plot([x for x, _ in timings_basic], [y for _, y in timings_basic])
plt.xlabel('Number of intervals')
plt.ylabel('Time (seconds)')

Text(0, 0.5, 'Time (seconds)')

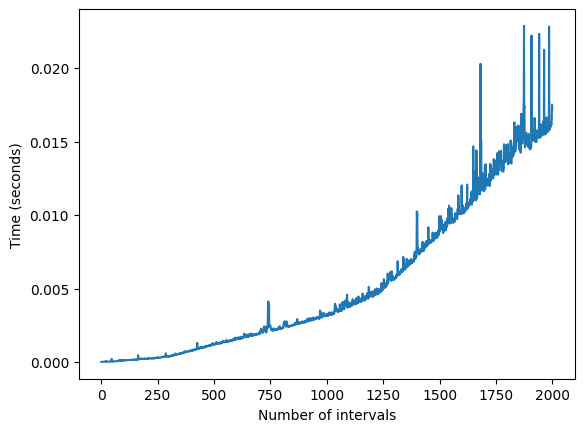
There is a quadratic progression.

The approach that solves this issue is realized in the function below. It simply finds the maximum simultanious intervals and then accounts and returns the set of elements it consists of.

def two_pass(intervals: list[tuple[int, int]]) -> set[int]:
    events = construct_events(intervals)
    events.sort()

    intervals_set: set[int] = set()

    count = 0
    max_count = 0
    # First pass to find the maximum number of overlapping intervals
    for _, e_type, _ in events:
        if e_type == START:
            count += 1
        else:  # e_type == END
            count -= 1
        max_count = max(max_count, count)

    # Second pass to find the indices of intervals with the maximum overlap
    for _, e_type, i in events:
        if e_type == START:
            intervals_set.add(i)
        else:  # e_type == END
            intervals_set.remove(i)
        if len(intervals_set) == max_count:
            return intervals_set
    return set()

The results of applying the same test applied to the two_pass is displayed below.

timings_two_passes = estimate_time_complexity(two_pass)

plt.plot([x for x, _ in timings_basic], [y for _, y in timings_basic])
plt.plot([x for x, _ in timings_two_passes], [y for _, y in timings_two_passes])
plt.xlabel('Number of intervals')
plt.ylabel('Time (seconds)')

Text(0, 0.5, 'Time (seconds)')

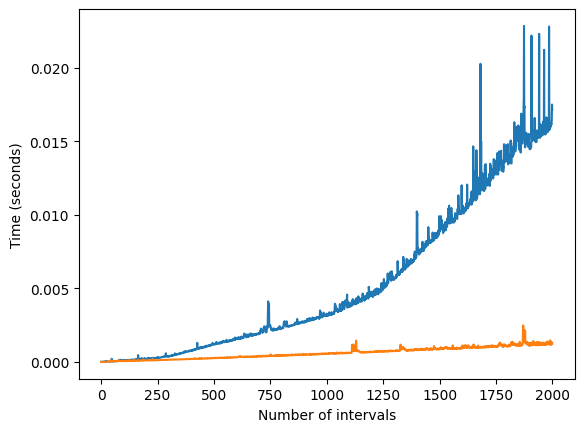
Even if the exact complexities of the algorithms are not obvious, the two_pass approach certainly has better results here.